Utility jobs
You can use the Data Catalog utility tools to update dashboards, and troubleshoot discovery and metadata details. Extended profiling generates resource metadata used for discoveries that reside in the discovery cache. Use the following tools to troubleshoot specific data in the discovery cache for qualifying discovery operations, updating dashboards, and resolving metadata inconsistencies.
Tools only appear in Manage if you have administrator permissions. These utilities are generally used with the LDC Agent component.
Maintaining the discovery cache (DiscoveryCacheCompactor)
Removes unused MapFile directories and merges small MapFile directories. It is a distributed replacement for
RepoCacheMaintenance.
Run a Data Rationalization job
Reports details about duplicated and overlapping data. Use this utility to populate the Data Rationalization dashboard.
Check lineage (lineage_check)
Reports details about inferred lineage between child and parent data resources. Use this utility to check if lineage can be discovered.
Check tag propagation (tag_check)
Reports details for tag association suggestions between specific resource field(s) and any tag in question. Use this utility to determine why a tag was not propagated.
Utils
You can perform the following actions on CSV files:
- Propagate information across the lineage relationships to show the origin of the data (OriginPropagation)
- Export all the lineages (ExportLineage)
- Import all lineages (ImportLineage)
Utils Yarn
You can perform the following actions with Utils Yarn:
- Calculate precise cardinalities and most frequent values (correctFrequency)
- Remove suggested tag-field associations (TFARemover)
The output size from some of these utilities may be large. As a best practice, you should redirect the console output to a temporary file.
Open and run a utility tool
Procedure
Navigate to Manage, then click Tools.
The Tools page opens.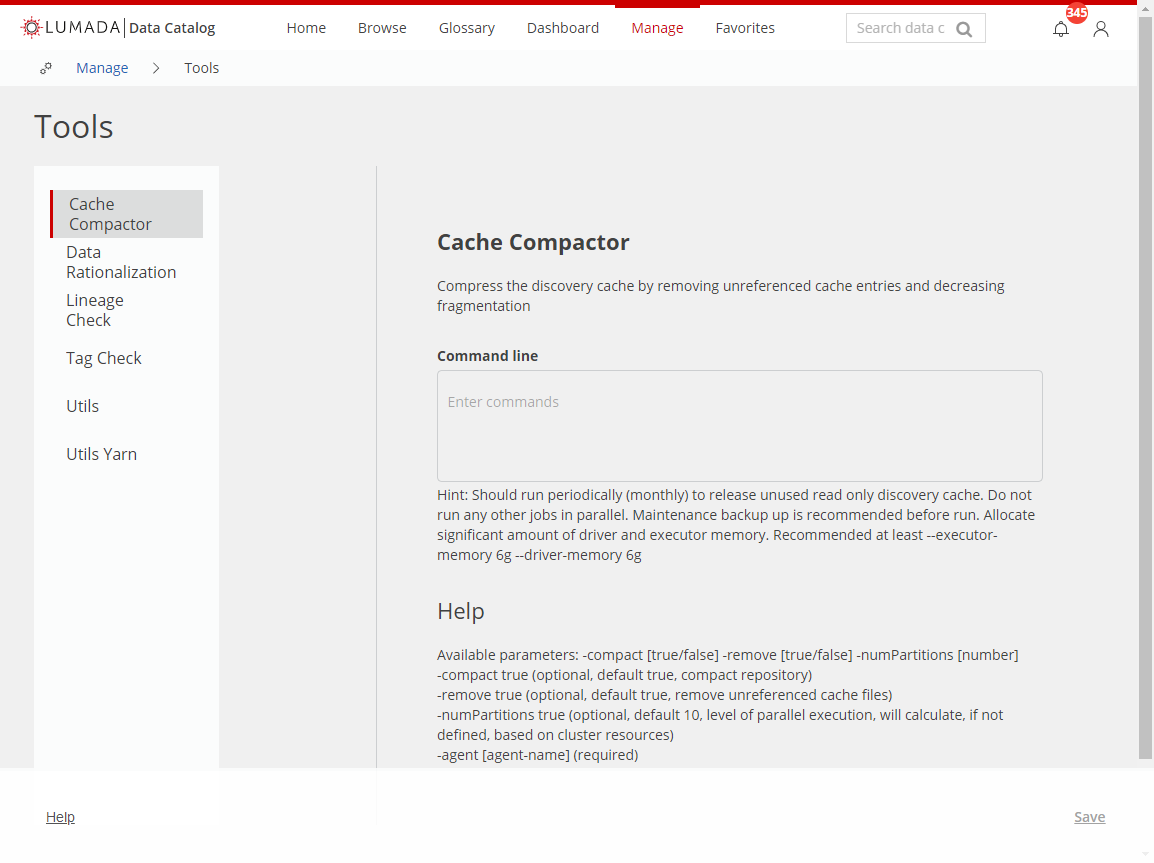 NoteTools only appears in Manage if you have administrator permissions.
NoteTools only appears in Manage if you have administrator permissions.From the Tools panel on the left, select the utility tool you want to use.
The dialog box updates with the tool you selected.Enter the utility parameters you want to set to your specific values in the Command line text box.
Click Submit job.
Results
Maintaining the discovery cache
As a best practice, you should maintain the discovery cache by removing unused MapFile directories and merging small MapFile directories. The Data Catalog discovery cache is a repository containing large properties of entities generated during profiling and tag propagation. Large properties are used in tag propagation, lineage discovery, and in some instances regular expression evaluation.
The location and content of the discovery cache are controlled by two properties in the configuration.json file:
ldc.metadata.hdfs.large_properties.uriDefines the URI of the discovery cache metadata files. Its default value is hdfs://<host>:8020.
ldc.metadata.hdfs.large_properties.pathDefines the location relative to the discovery cache URI of the discovery cache metadata store. Its default value is /user/ldcuser/.ldc_hdfs_metadata.
You should change the URI and location to fit your environment, and both should be accessible by the user running jobs.
The large properties of data resources and tag propagation information in the discovery cache are stored in the resource_lp and tag_lp directories.
To view the metadata for tag and large properties, enter the following command:
$ hdfs dfs -ls /user/ldcuser/.ldc_hdfs_metadata/
The output is similar to the following example:
$ hdfs dfs -ls /user/ldcuser/.ldc_hdfs_metadata/ Found 3 items drwxr-xr-x - ldcuser ldcuser 0 2021-09-28 05:25 /user/ldcuser/.ldc_hdfs_metadata/Built-in_Tags drwxr-xr-x - ldcuser ldcuser 0 2021-09-28 05:45 /user/ldcuser/.ldc_hdfs_metadata/resource_lp drwxr-xr-x - ldcuser ldcuser 0 2021-09-28 05:45 /user/ldcuser/.ldc_hdfs_metadata/tag_lp $
Each directory contains the map files with generated unique names.
$ hdfs dfs -rm -R /user/ldcuser/.ldc_hdfs_metadata
Compression is controlled by configuration parameters, as shown in the following examples:
ldc.metadata.discovery.cache.unreferenced
"ldc.metadata.discovery.cache.unreferenced":{ "value": 50.0, "type": "FLOAT", "restartRequired": false, "readOnly": false, "description": "if below this percentage, the objects from mapfile will be relocated during discovery cache compacton (DiscoveryCacheCompactor).", "label": "percent of discovery cache unreferenced objects in one mapfile", "category": "DISCOVERY", "defaultValue": 50.0, "visible": false }ldc.discovery.cache.objects.min
"ldc.discovery.cache.objects.min": { "value": 50 "type": "INTEGER", "restartRequired": false, "readOnly": false, "description": "If below this number, the object from MapFile will be relocated during discovery cache compaction(DiscoveryCacheCompactor).", "label": "Minimum number of objects in discovery cache MapFile", "category": "DISCOVERY", "defaultValue": 50, "visible": false }
Compress the discovery cache
Procedure
Navigate to Tools under Manage, then click Cache Compactor.
The Cache Compactor page opens.Enter the following parameters you want to specify in the Command line text box, referencing the following command syntax examples:
Syntax example 1
-numPartitions 4 -remove true -compact true -agent {agentname}Syntax example 2
– agent {agentName}-agentAgent name.
-compact(Optional) If set to true, small or partially referenced discovery cache map file directories are merged according to
ldc.metadata.discovery.cache.unreferencedandldc.discovery.cache.objects.minconfigurations. If set to false, the directories are reported, not merged. The default value is true.-remove(Optional) If set to true, unreferenced discovery cache files are removed. If set to false, unreferenced discovery cache files are reported, not removed.
-numPartitions(Optional) Number of partitions. The default value is 10.
Click Submit job.
Results
Run a Data Rationalization job
Before you run a Data Rationalization job, you must first run the applicable profile, discovery, and lineage jobs on your data. Also, allocate at least 6 GB of memory for the executors and driver for this job.
Perform the following steps to run a Data Rationalization job:
Procedure
Navigate to Tools under Manage, then click Data Rationalization.
Add any of the following parameters and values to the Command line text box according to your requirements.
NoteAll parameters are optional. If a value is not specified, the default value is used.Parameter Description -firstDataSource Specifies the first data source to use for overlap analysis. If not defined, all data sources are analyzed. -secondDataSource Specifies the second data source to use for overlap analysis. If the second data source is not defined, all data sources are analyzed. -incremental Specifies whether to perform incremental analysis. Set to true to perform overlap analysis for data sources only if the analysis has not been done before or requires an update. Set to false to redo the overlap analysis. The default is true.
-reprocess Specifies whether to reprocess data resources. Set to true to perform overlap analysis for data resources that have been processed. Set to false to perform overlap analysis only for resources that were re-profiled after the last analysis. The -incremental parameter must be set to false for this parameter to be active. The default is false.
-fth_copy Specifies the amount of overlap ratio when assessing a field as a copy. The formula is (1.0 - cardinality ratio < -fth_copy value). The default is 0.1.
-fth_overlap Specifies the precision to cut off accidental field overlaps. The file is considered an overlap if both the source and target overlap ratios are greater than this value. The default is 0.2..
-rth_copy Specifies the amount of precision required to detect if resources are copies. Resources are assessed as copies if the ratio of the matching fields in the compared resources is less than this value. The default is 0.1.
-rth_overlap Specifies the precision in overlap relationships needed to cut off accidental resource overlaps. Overlap relationships are denoted between resource1 and resource2 only if max([resource1 overlapped fields count]/[resource1 fields count], [resource2 overlapped fields count]/[resource2 fields count]) > [this value].The default is 0.32.
-same_semantics Specifies whether to perform semantic analysis. Set to true to perform overlap analysis for a pair of source and target fields that have the same internally discovered semantics attributes, such as temporal,free text,numeric, orstrings. To extend the scope of fields compared for overlap analysis, set this value to false. Setting this value to false may increase the accuracy of your overlap analysis, but also may cause a decrease in performance.The default is true.
-exclude_field_list Specifies a list of field names to exclude from overlap analysis. Click Save.
Results
Next steps
Check lineage
Perform the following steps to report the suitability of two resources as candidates for a lineage relationship:
Procedure
Navigate to Tools under Manage, then click Lineage Check.
The Lineage Check page displays.Enter the following parameters you want to specify in the Command line text box:
-agentAgent name.
-parentVirtualFolderName of the parent virtual folder.
-parentDataResourceA fully qualified path to parent data resource.
-childVirtualFolderName of child virtual folder.
-childDataResourceA fully qualified path to child data resource.
-validation(Optional) If set to true, the significance of parent-child relationship is validated using modification timestamps for HDFS and HIVE data resources. The default value is true.
Click Submit job.
Results
Example 1
This example shows the parameters set to check lineage for the /user/demo/raw/rest_insp/restaurants_nyc.csv data resource and its child data resource /user/demo/pub/classified/blended_violations.csv:
-parentVirtualFolder MySource -parentDataResource /user/demo/raw/rest_insp/restaurants_nyc.csv -childVirtualFolder MySource -childDataResource /user/demo/pub/classified/blended_violations.csv
Example 2
This example shows the parameters set to check lineage for the /default.table1 data resource and its child data resource /default.table1_vw:
-parentVirtualFolder MyHIVE -parentDataResource /default.table1 -childVirtualFolder MyHIVE -childDataResource /default.table1_vw
Check tag propagation
Perform the following steps to report on tag association suggestions:
Procedure
Navigate to Tools under Manage, then click Tag Check.
The Tag Check page displays.Enter the following parameters you want to specify in the Command line text box:
-agentAgent name.
-virtualFolderVirtual folder name.
-dataResourceA fully qualified path to data resource.
-domainTag domain name to which the tag belongs. You may use the shortcut
-domain pfor the Built-in_Tags domain.-tagTag name for which propagation is being checked.
-field(Optional) Full path to field. If this parameter is not set, all fields are checked.
Click Submit job.
Results
-virtualFolder MyHDFS -dataResource /user/ldcuser/lineage/filter/superset/parent/filter_superset_parent.csv -domain Built-in_Tags -tag Country -field Country -agent LocalAgent
Examine data resource origins
You can use the OriginPropagation utility tool to examine origins in the single resource view.
Perform the following steps to investigate origin propagations across lineage relationships:
Procedure
Navigate to Tools under Manage, then click Utils.
The Utils page opens.Enter the following parameters you want to specify into the Command line text box, referencing the following command syntax examples:
Example Syntax 1
-driver com.hitachivantara.datacatalog.origin.OriginPropagation -mode inferred -agent LocalAgentExample Syntax 2
-driver com.hitachivantara.datacatalog.origin.OriginPropagation -mode factual -agent LocalAgent-agentAgent name. This parameter is only required if multiple agents are registered.
-driverThe driver of the utility. For origin propagation, set
-drivertocom.hitachivantara.datacatalog.origin.OriginPropagation.-modeThe type of origin. Specify one of the following options to propagate the selected type of origin:
inferred
Include only origins through inferred (accepted and suggested) lineages.
imported
Include only origins through factual imported lineages.
all
(default) Include origins through all lineages (inferred and imported).
Click Submit job.
Results
Lineage export and import
You can export lineages discovered by Data Catalog and import user-defined lineages with the lineage export and import utility. You can also use the utility to delete lineages that were exported as a CSV file with the ExportLineage action.
The lineage relationships, both resource level and field level, are exported in the CSV format in a pre-defined structure. Lineage import also requires the user-defined lineages to be submitted only in this pre-defined format. Lineage export and imports are based on lineage targets, not sources.
When limiting lineage export to a specific virtual folder or path, all lineages are exported to defined targets in the virtual folder or path.
Export-import CSV structure
Data Catalog exports lineages in a pre-defined fixed format. The following table describes the columns of this fixed format:
| Col# | Col Name | Default Value | Description |
| A | external_id | system generated | (Required) Unique ID of the entity represented by CSV line, operation, or operation execution |
| B | external_source_name | "LDC" | Name of the external source. Use LDC for lineages created manually in Data Catalog. |
| C | target_data_source_name | "" | Name of the target data source |
| D | target_resource_path | "" | Target data resource path |
| E | lineage_type | "" | Lineage type (options: INFERRED, INFERRED_ALTERNATIVE, FACTUAL, IMPORTED, HDFS2HIVE, OTHER) |
| F | lineage_kind | "" | Lineage kind (options: COPY, PARTIAL_COPY, JOIN, UNION, UNION_PART, MASK, ENCRYPT, STANDARDIZE, CALCULATION, SUBSET, SUPERSET, HIVE_EXTERNAL, OTHER) |
| G | lineage_exec_type | "" | Lineage operation level (options:
lineage_exec_type_resource,
lineage_exec_type_field) |
| H | target_resource_field | "" | Target field |
| I | resource_lineage_reference | "" | GUID for the Operation execution entity GUID |
| J | principal | "" | Principal or lineage creator as group:user |
| K | source_data_source_name | "" | Source data source name |
| L | source_resource_path | "" | Source data resource path |
| M | source_resource_field | "" | Source field |
| N | lineage_state | "" | Lineage state (options: ACCEPTED, REJECTED, SUGGESTED, IMPORTED) |
| O | description | "" | Lineage description |
| P | code | "" | Transformation code |
| Q | operation_reference | "" | GUID for the Operation entity |
| R | operation_type | "operation_execution" | Lineage entity type (options: operation, operation_execution). The default value is operation_execution. |
For every lineage you export, the details for the lineage operation include the operation execution details, as shown in the following example:
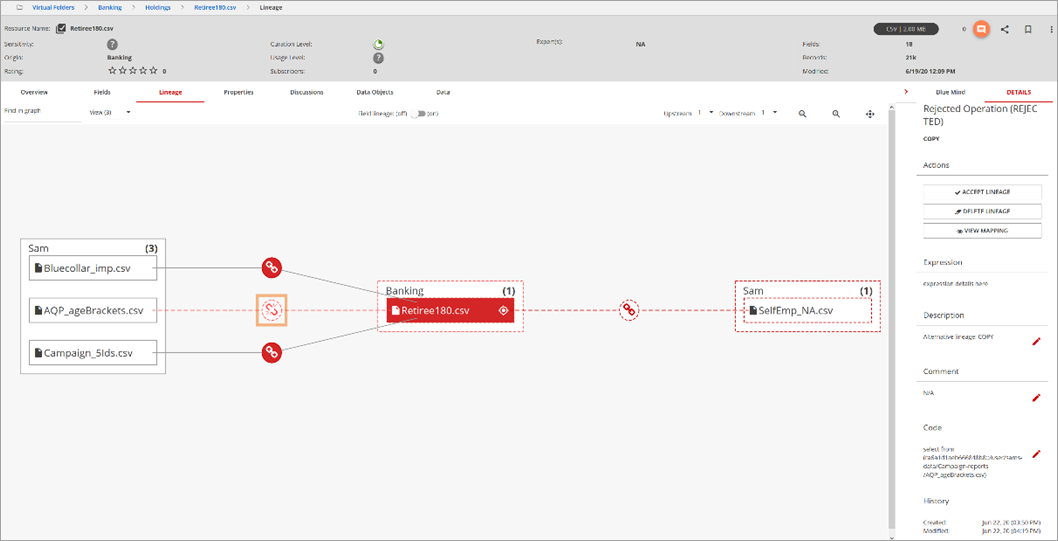
The following sample is a portion of the CSV file exported from the example above:

The following details apply to the selected sample of the CSV export:
- Row 75: Identifies the lineage and shows it was REJECTED.
- Row 76: Lists all the information in the DETAILS panel for the lineage. It identifies lineage type, kind, status, description, and code.
- Rows 77 – 94: Lists the field level lineage details for the selected lineage operation. The Code column (Col P) identifies the source field to target field mapping found in the View Mapping or Code section under the DETAILS tab.
The operation_reference values (Column Q in this example) for
all rows following the lineage identifier row (Row 75 per this example) are the same and
represent the external_id of the lineage operation.
The following lineage types can occur:
Inferred
Primary lineage discovered by Data Catalog. The AI engine identifies one primary lineage based on proprietary algorithms.
Inferred alternative
Lineage discovered by Data Catalog. If more than one source is a candidate for primary lineage, the AI engine marks these inferred lineages as
Inferred_alternative.Factual
Any lineage added manually.
Imported
Any lineage imported from third-party applications such as Atlas or Navigator.
HDFS2HIVE
HDFS to HIVE lineage identified as part of schema discovery.
Export a lineage
Procedure
Navigate to Tools under Manage, then click Utils.
The Utils page opens.Enter the following parameters you want to specify into the Command line text box:
-agentAgent name. This parameter is only required if multiple agents are registered.
-driverThe driver of the utility. For origin propagation, set
-drivertocom.hitachivantara.datacatalog.lineage.ExportLineage.-fileA name string for the CSV file, which will be generated with the export action.
-virtualFolder(Optional) Limit the lineage export to this virtual folder. If this parameter is not set, all lineages in the data lake are exported.
-path(Optional) Limit the lineage export to this path.
-separator(Optional) Separators used in the exported CSV file. The default value is
','.
Click Submit job.
Results
-driver com.hitachivantara.datacatalog.lineage.ExportLineage -agent localAgent -file /home/ldcuser/lineage-utility/Exported-lineage.csv
The output of the above command displays heartbeat style messages for every 50 lineages processed, and identifies the total number of lineages processed, as in the following sample:
INFO | 2020-04-10 02:24:06,563 | | Main [main] - Starting Lumada Data Catalog 2019.3 Build:420 Patch:undefined with Oracle Corporation Java, Version 1.8.0_112 from /usr/jdk64/jdk1.8.0_112/jre, Locale en_US
INFO | 2020-04-10 02:24:06,564 | | Main [main] - Arguments [-action, utils, -driver, com.hitachivantara.lineage.ExportLineage, -file, /home/ldcuser/lineage-utility/Exported-lineage.csv]
INFO | 2020-04-10 02:24:06,583 | utils | ClientConfigurationLoader [main] - In loadConfig Loading configuration from file: meta-client-configuration.json
INFO | 2020-04-10 02:24:06,660 | utils | MetadataClientServicefactory [main] - Preparing metadataclient
INFO | 2020-04-10 02:24:06,713 | utils | Main [main] - Calling com.hitachivantara.lineage.ExportLineage with options {action=utils, file=/home/ldcuser/lineage-utility/Exported-lineage.csv, COMMAND=/opt/ldc/agent/bin/ldc utils -virtualFolder null -path null}.
WARN | 2020-04-10 02:24:06,719 | utils | LockManager [main] - Zookeeper based locking is disabled. Jobs should not be run concurrently
INFO | 2020-04-10 02:24:06,719 | utils | ExportLineage [main] - Getting metadata client instance.
INFO | 2020-04-10 02:24:06,719 | utils | MetadataClientServicefactory [main] - Preparing metadataclient
INFO | 2020-04-10 02:24:06,719 | utils | ExportLineage [main] - Utility parameters validated.
Virtual folder: [null]
Path: [null]
File: [/home/ldcuser/lineage-utility/Exported-lineage.csv]
Field delimiter: [,]
INFO | 2020-04-10 02:24:06,719 | utils | ExportLineage [main] - Starting to export lineage information.
INFO | 2020-04-10 02:24:06,719 | utils | ExportLineage [main] - Fetching all lineages.
INFO | 2020-04-10 02:24:38,127 | utils | ExportLineage [main] - Successfully processed 50 lineages so far...
INFO | 2020-04-10 02:25:12,254 | utils | ExportLineage [main] - Successfully processed 100 lineages so far...
INFO | 2020-04-10 02:25:40,729 | utils | ExportLineage [main] - Successfully processed 150 lineages so far...
INFO | 2020-04-10 02:25:55,552 | utils | ExportLineage [main] -
Finish lineage export. 189 lineages were successfully exported to file /home/ldcuser/lineage-utility/Exported-lineage.csv. Encounter 0 errors
INFO | 2020-04-10 02:25:55,554 | utils | ExportLineage [main] -
Elapsed time = PT1M48.832S
INFO | 2020-04-10 02:25:55,554 | utils | ExportLineage [main] - Successfully exported all lineages.
INFO | 2020-04-10 02:25:55,554 | utils | Main [main] - Elapsed time PT1M49.53S
INFO | 2020-04-10 02:25:55,554 | utils | Main [main] -
Import a lineage
Procedure
Navigate to Tools under Manage, then click Utils.
The Utils page opens.Enter the following parameters for com.hitachivantara.datacatalog.lineage.ImportLineage in the Command line text box:
-agentAgent name. This parameter is only required if multiple agents are registered.
-driverThe driver of the utility. For origin propagation, set
-drivertocom.hitachivantara.datacatalog.lineage.ImportLineage.-file(Required) The path to the CSV file that will be imported.
-separator(Optional) Separators used in the CSV file, except for the pipe character (‘
|’). The default value is','.-replaceConfig(Optional) CSV file with configured replacements. You can use the configuration file to make replacements to the lineages during the import process. See Replacing lineages during import for details.
-undo(Optional) When set to true, all defined lineages are removed in the import file specified. The default value is false.
Click Submit job.
Results
Next steps
Lineage best practices
You should adhere to the following best practices when updating existing lineages in Data Catalog.
- You can update existing lineages by exporting them to a CSV file, curating the lineages in the CSV file, then importing the transformed lineages back into Data Catalog.
- When updating lineages, do not manipulate the
external_id,lineage_exec_type,resource_lineage_referenceoroperation_referencefields. Errors occur when any of these fields are modified.- The
external_ids are generated by Data Catalog and are unique to the system. - The
lineage_exec_typefield identifies resource lineage versus field lineage. - The
resource_lineage_referenceandoperation_referencefields depend on theexternal_idfield.
- The
- The
principal,description, andcodefields are descriptive. No validations are performed on the content of these fields while importing lineages. - The
lineage_typeandlineage_kindfields are also considered descriptive when importing lineages. No validations are performed on the user updates to these fields. - Validations are performed on any changes to the
target_data_source_namefield, thesource_data_source_namefield, the target path, the target field, the resource path, the resource field, and thelineage_state. Changes to resource names as part of path name changes are not supported. - Data Catalog does not offer field curation.
Removing lineages
You can also use the export-import lineage utility to remove lineages from Data Catalog. When the undo option of the ImportLineage action is set to true, it removes all lineages specified in the import CSV file, as shown in the following example command:
-driver com.hitachivantara.datacatalog.lineage.ImportLineage -file ~ldcuser/Exported-Lineage/export_apr2020.csv -undo true
Replacing lineages during import
You can use the Replace-config file to make replacements to lineages during the import process. Use the optional parameter -replaceConfig to use the file to make replacements to the lineages when importing the CSV lineages. See Import a lineage for the command syntax.
For example, in the environment where the CSV lineages are imported, the paths to specific resources are different. One option is to manually edit the CSV lineage file to alter any or every occurrence of the specified resource. In another example, where mapping an account field of one resource to the record field of another resource downstream, a resource may be more applicable according to business logic than mapping it to the account field in that resource. You can search and make those changes in the CSV lineage file.
The Replace-config file automates these replacements in run-time when the import command is triggered. The Replace-config file is a CSV file with the following comma-separated (",") fields:
| Column | Column Name | Description |
| A | field name from CSV header | (Required) Name of the field being replaced (from the CSV header). |
| B | value to be replaced | (Required) Value to be replaced. |
| C | new value (replacement) | (Optional) Replacement value. The value is empty if it is not defined. |
| D | replacement strategy |
(Optional) One of the four following values:
|
The following sample is an example Replace-config file:
principal,,wlddev:wldservice-user target_data_source_name,COPY,LANDING,ALL target_resource_path,/user/wlddev/lin_ju_stg/SRC_JOIN2,/user/wlddev/lin_ju_stg/SRC_JOIN,START target_resource_path,/user/wlddev/lin_ju_src/SRC_JOIN2,/user/wlddev/lin_ju_src/SRC_JOIN,START target_resource_path,TRG_JOIN2,TRG_JOIN,OCCURRENCE source_data_source_name,COPY,LANDING,ALL source_resource_path,/user/wlddev/lin_ju_stg/SRC_JOIN2,/user/wlddev/lin_ju_stg/SRC_JOIN,START source_resource_path,/user/wlddev/lin_ju_src/SRC_JOIN2,/user/wlddev/lin_ju_src/SRC_JOIN,START source_resource_path,TRG_JOIN2,TRG_JOIN,OCCURRENCE
Correct frequency
Perform the following steps to modify the frequency of precise calculations:
Procedure
Navigate to Tools under Manage, then click Utils Yarn.
The Utils Yarn page opens.Enter the following parameters you want to specify in the Command line text box:
-agentAgent name. This parameter is only required if multiple agents are registered.
-driverThe driver of the utility. For origin propagation, set
-drivertocom.hitachivantara.datacatalog.cli.MostFrequentCounter.-virtualFolder(Optional) Data resources from this virtual folder. If this parameter is not set, all applicable data resources from the repository are used.
-path(Optional) Profiling path (resource specific filter). By default, the entire virtual folder is used.
-min_card(Optional) Minimum reported cardinality to recalculate the most frequent distribution for the fields. The default value is 500000.
-min_topk_count(Optional) Minimum most frequent reported count to recalculate the most frequent distribution for the fields. The default value is 16.
-calc_card(Optional) If set to true, recalculate the precise cardinality for the fields selected for the most frequent distribution recalculation. The default value is true.
-lines_out(Optional) Top most frequent values for the old and new exact distribution. The default value is 20.
Click Submit job.
Results
Remove tag field associations
Procedure
Navigate to Tools under Manage, then click Utils Yarn.
The Utils Yarn page opens.Enter the following parameters you want to specify in the Command line text box, referencing the following command syntax examples:
Example Syntax 1
-driver com.hitachivantara.datacatalog.cli.bucket.TFARemover -domain Built-in_Tags sfa true -agent LocalAgent
Example Syntax 2
-driver com.hitachivantara.datacatalog.cli.bucket.TFARemover -domain Built-in_Tags sfa false -agent LocalAgentExample Syntax 3
-driver com.hitachivantara.datacatalog.cli.bucket.TFARemover -domain Custom_domain sfa true -agent LocalAgentExample Syntax 4
-driver com.hitachivantara.datacatalog.cli.bucket.TFARemover -domain Custom_domain sfa false-agent LocalAgentExample Syntax 5
-driver com.hitachivantara.datacatalog.cli.bucket.TFARemover -domain Built-in_Tags -agent LocalAgent-agentAgent name. This parameter is only required if multiple agents are registered.
-driverThe driver of the utility. For origin propagation, set
-drivertocom.hitachivantara.datacatalog.cli.bucket.TFARemover.-domainTag domain name.
-tag(Optional) Tag name. Removes all suggested tag associations for this tag. If the domain is manually created, Data Catalog removes suggested tag associations. If the tag name is not defined, all suggested tags from the domain are removed.
Click Submit job.
Results

